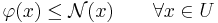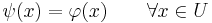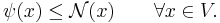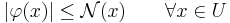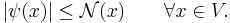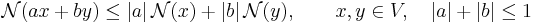Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed vector space to make the study of the dual space "interesting." Another version of Hahn–Banach theorem is known as Hahn-Banach separation theorem or the separating hyperplane theorem, and has numerous uses in convex geometry. It is named for Hans Hahn and Stefan Banach who proved this theorem independently in the late 1920s, although a special case [1] was proved earlier (in 1912) by Eduard Helly,[2] and a general extension theorem from which the Hahn–Banach theorem can be derived was proved in 1923 by Marcel Riesz.[3]
Contents |
Formulation
The most general formulation of the theorem needs some preparation. Given a vector space V over the field R of real numbers, a function ƒ : V → R is called sublinear if
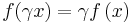 for any
for any 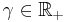 and any x ∈ V (positive homogeneity),
and any x ∈ V (positive homogeneity),
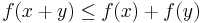 for any x, y ∈ V (subadditivity).
for any x, y ∈ V (subadditivity).
Every seminorm on V (in particular, every norm on V) is sublinear. Other sublinear functions can be useful as well, especially Minkowski functionals of convex sets.
The Hahn–Banach theorem states that if
is a sublinear function, and
is a linear functional on a linear subspace U ⊆ V which is dominated by
on U,
then there exists a linear extension
of
to the whole space V, i.e., there exists a linear functional ψ such that
and
(Rudin 1991, Th. 3.2)
Another version of Hahn–Banach theorem states that if V is a vector space over the scalar field K (either the real numbers R or the complex numbers C), if 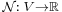 is a seminorm, and
is a seminorm, and 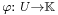 is a K-linear functional on a K-linear subspace U of V which is dominated by
is a K-linear functional on a K-linear subspace U of V which is dominated by 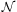 on U in absolute value,
on U in absolute value,
then there exists a linear extension 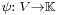 of φ to the whole space V, i.e., there exists a K-linear functional ψ such that
of φ to the whole space V, i.e., there exists a K-linear functional ψ such that
and
In the complex case of this theorem, the C-linearity assumptions demand, in addition to the assumptions for the real case, that for every vector x ∈ U, the vector i x be also in U and φ(i x) = i φ(x).
The extension ψ is in general not uniquely specified by φ, and the proof gives no explicit method as to how to find ψ: in the case of an infinite dimensional space V, it depends on Zorn's lemma, one formulation of the axiom of choice.
It is possible to relax slightly the sublinearity condition on 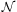 , requiring only that
, requiring only that
according to (Reed and Simon, 1980). This reveals the intimate connection between the Hahn–Banach theorem and convexity.
The Mizar project has completely formalized and automatically checked the proof of the Hahn–Banach theorem in the HAHNBAN file.
Important consequences
The theorem has several important consequences, some of which are also sometimes called "Hahn–Banach theorem":
- If V is a normed vector space with linear subspace U (not necessarily closed) and if φ : U → K is continuous and linear, then there exists an extension ψ : V → K of φ which is also continuous and linear and which has the same norm as φ (see Banach space for a discussion of the norm of a linear map). In other words, in the category of normed vector spaces, the space K is an injective object.
- If V is a normed vector space with linear subspace U (not necessarily closed) and if z is an element of V not in the closure of U, then there exists a continuous linear map ψ : V → K with ψ(x) = 0 for all x in U, ψ(z) = 1, and ||ψ|| = 1 / dist(z, U).
- In particular, if V is a normed vector space and if z is any element of V, then there exists a continuous linear map ψ : V → K with ψ(z) = ||z|| and ||ψ|| ≤ 1. This implies that the natural injection J from a normed space V into its double dual V ′′ is isometric.
Hahn-Banach separation theorem
Another version of Hahn–Banach theorem is known as the Hahn-Banach separation theorem.[4] It has numerous uses in convex geometry,[5] optimization theory, and economics. The separation theorem is derived from the original form of the theorem.
Theorem: Let V be a topological vector space over 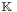 = ℝ or ℂ, and A, B convex, non-empty subsets of V. Assume that A ∩ B = ∅. Then
= ℝ or ℂ, and A, B convex, non-empty subsets of V. Assume that A ∩ B = ∅. Then
(i) If A is open, then there exists a continuous linear map 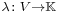 and
and 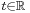 such that
such that 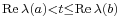 for all
for all  ,
, 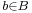
(ii) If V is locally convex, A is compact, and B closed, then there exists a continuous linear map 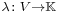 and
and 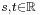 such that
such that 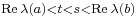 for all
for all  ,
, 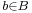 .
.
Relation to the axiom of choice
As mentioned earlier, the axiom of choice implies the Hahn–Banach theorem. The converse is not true. One way to see that is by noting that the ultrafilter lemma, which is strictly weaker than the axiom of choice, can be used to show the Hahn–Banach theorem, although the converse is not the case. The Hahn–Banach theorem can in fact be proved using even weaker hypotheses than the ultrafilter lemma.[6] For separable Banach spaces, Brown and Simpson proved that the Hahn–Banach theorem follows from WKL0, a weak subsystem of second-order arithmetic that takes König's Lemma as an axiom.[7]
See also
Notes
- ^ for the space C[a, b] of continuous functions on an interval
- ^ O'Connor, John J.; Robertson, Edmund F., "Hahn–Banach theorem", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Helly.html.
- ^ See M. Riesz extension theorem. According to Gȧrding, L. (1970). "Marcel Riesz in memoriam". Acta Math. 124 (1): I-XI. MR0256837., the argument was known to Riesz already in 1918.
- ^ Gabriel Nagy, Real Analysis lecture notes
- ^ Harvey, R.; Lawson, H. B. (1983). "An intrinsic characterisation of Kahler manifolds". Invent. Math 74 (2): 169–198. doi:10.1007/BF01394312.
- ^ Pincus, D. (1974). "The strength of Hahn–Banach's Theorem". Victoria Symposium on Non-standard Analysis. Lecture notes in Math.. 369. New York: Springer. pp. 203–248. ISBN 038706656X. Citation from Foreman, M.; Wehrung, F. (1991). "The Hahn-Banach theorem implies the existence of a non-Lebesgue measurable set". Fundamenta Mathematicae 138: 13–19. http://matwbn.icm.edu.pl/ksiazki/fm/fm138/fm13812.pdf.
- ^ Brown, D. K.; Simpson, S. G. (1986). "Which set existence axioms are needed to prove the separable Hahn-Banach theorem?". Annals of Pure and Applied Logic 31: 123–144. doi:10.1016/0168-0072(86)90066-7. Source of citation.
References
- Lawrence Narici and Edward Beckenstein, "The Hahn–Banach Theorem: The Life and Times", Topology and its Applications, Volume 77, Issue 2 (1997) Pages 193-211.
- Michael Reed and Barry Simon, Methods of Modern Mathematical Physics, Vol. 1, Functional Analysis, Section III.3. Academic Press, San Diego, 1980. ISBN 0-12-585050-6.
- Rudin, Walter (1991), Functional Analysis (2nd ed.), McGraw-Hill Science/Engineering/Math, ISBN 978-0-07-054236-5
- Terence Tao, The Hahn–Banach theorem, Menger’s theorem, and Helly’s theorem